Tan 2x double angle formula 290838-Tan 2x double angle formula

Tan2x Formula Tan2x Formula Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved exampleSum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be used Truly obscure identities These are just here for perversity No, not$\begingroup$ The doubleangle formula for tangent would probably be helpful Do you know it?

Section 6 3 Double Angle And Half

Tan 2x double angle formula

Tan 2x double angle formula-= 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;It is called tan double angle identity and used as a formula in two cases Tan of double angle is expanded as the quotient of twice the tan function by subtraction of square of tan function from one The quotient of twice the tan function by subtraction of square of tan function from one is simplified as tan of double angle

Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube

Learn how use the double angle identities to solve trigonometric equations When we have equations with a double angle we will apply the identities to creat Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes Verify the identity `1/(tan^2x) 1/(cot^2x) = csc^2x sec^2x` 22tanx/1tan^2x YOU MIGHT ALSO LIKE Reciprocal, Quotient, and Pythagorean Identities 8 terms jessgac00 Trigonometric Identities some 35 terms baaskat000 trigometric identities Start The doubleangle formulas are summarized as follows sin(2θ) = 2sinθcosθ cos(2θ) = cos2θ − sin2θ = 1 − 2sin2θ = 2cos2θ − 1 tan(2θ) = 2tanθ 1 − tan2θ How to Given the tangent of an angle and the quadrant in which it is located, use the doubleangle formulas

Trigonometric Formulas like Sin 2x, Cos 2x, Tan 2x are known as double angle formulas because these formulas have double angles in their trigonometric functions Let's discuss Tan2x Formula Tan2x Formula = 2 tan x 1 − t a n 2 x Let's know how to derive the double angle tan2x formulaThe formulas for double angle identities are as follows If given one trigonometric function, its value, and its quadrant, you can find the exact value of every double angle identity For example, if told to find the exact value of sin2u given $\text {sec (u)}=\frac {9} {2}$, for $0\leq\text {u}\leq\frac {\pi} {2}$ (u is in quadrant 1) You mayCombining this formula with the Pythagorean Identity, cos 2 (x) sin 2 (x) = 1, two other forms appear cos(2x) = 2cos 2 (x) − 1 and cos(2x ) = 1 − 2sin 2 (x) The derivation of the double angle identities for sine and cosine, followed by some examples

The tangent of half of an acute angle of a right triangle whose sides are a Pythagorean triple will necessarily be a rational number in the interval (0, 1) Vice versa, when a halfangle tangent is a rational number in the interval (0, 1), there is a right triangle that has the full angle and that has side lengths that are a Pythagorean tripleVerify the identity 1 cos 2x tan x = sin 2x Use the appropriate doubleangle formulas to rewrite the numerator and dena simplified 1 cos 2x sin 2x 1 Simplify the numerator Enter denominator found in the previ The expression from the previous step then simplifies to tan x using what?The double angle formulas can be derived by setting A = B in the sum formulas above For example, sin(2A) = sin(A)cos(A) cos(A)sin(A) = 2sin(A)cos(A) It is common to see two other forms expressing cos(2A) in terms of the sine and cosine of the single angle A Recall the square identity sin 2 (x) cos 2 (x) = 1 from Sections 14 and 23

Trig Angle Addition Identities Video Khan Academy

Half Angle Identities

O A Pythagorean Identity OB Quotient Identity OCThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Using the double angle identity for cosine cos 2 x = cos 2 x − sin 2 x cos 2 x = ( 1 − sin 2 x) − sin 2 x cos 2 x = 1 − 2 sin 2 x This expression is an equivalent expression to the double angle identity and is often considered an alternate form Example 342 5 Simplify the following identity sin 4 x − cos 4 x

Sin 2 X Identities Regan Cletus

Ppt Double Angle And Half Angle Formulas Powerpoint Presentation Free Download Id

Derivation of the Double Angle Formulas The Double Angle Formulas can be derived from Sum of Two Angles listed below $\sin (A B) = \sin A \, \cos B \cos A \, \sin B$ → Equation (1)Formula for Lowering Power tan^2 (x)=?Following table gives the double angle identities which can be used while solving the equations You can also have sin2θ,cos2θ expressed in terms of tanθ as under sin2θ = 2tanθ 1

Trigonometric Identities Ppt Download

Section 7 3 Double Angle Half Angle And Sum

 Formulas expressing trigonometric functions of an angle 2x in terms of functions of an angle x, sin(2x) = 2sinxcosx (1) cos(2x) = cos^2xsin^2x (2) = 2cos^2x1 (3) = 12sin^2x (4) tan(2x) = (2tanx)/(1tan^2x) (5) The corresponding hyperbolic function doubleangle formulas are sinh(2x) = 2sinhxcoshx (6) cosh(2x) = 2cosh^2x1 (7) tanh(2x) = (2tanhx)/(1tanh^2x) The double angle formula, is the method of expressing Sin 2x, Cos 2x, and Tan 2x in congruent relationships with each other In this lesson, we will seek to prove on aCos 2x ≠ 2 cos x;

Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf

Double Angle Formula Sine Cosine And Tangent Owlcation

8 Given tan x= 7 find the exact value of tan 2x You must use a doubleangle formula Show all work Write your work on paper, take pictures and submit them in Blackboard Question 8 Given tan x= 7 find the exact value of tan 2x You must use a doubleangle formula0/2 Points DETAILS PREVIOUS ANSWERS SPRECALC6 Find sin 2x, cos 2x, and tan 2x from the given information Functions sec x B x in Quadrant N X Symbols MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER cale sin 2r = H q Relations Sets Simplify the expression by using a DoubleAngle Formula or a HalfAngle Formula Function cos 2r Vi o!Double angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin ⁡ 2 x = 1 2 ( 1 − cos ⁡ 2 x) cos ⁡ 2 x = 1 2 ( 1 cos ⁡ 2 x) sin ⁡ x cos ⁡ x = 1 2 ( sin ⁡ 2 x) tan ⁡ 2 x = 1 − cos ⁡ 2 x 1 cos ⁡ 2 x

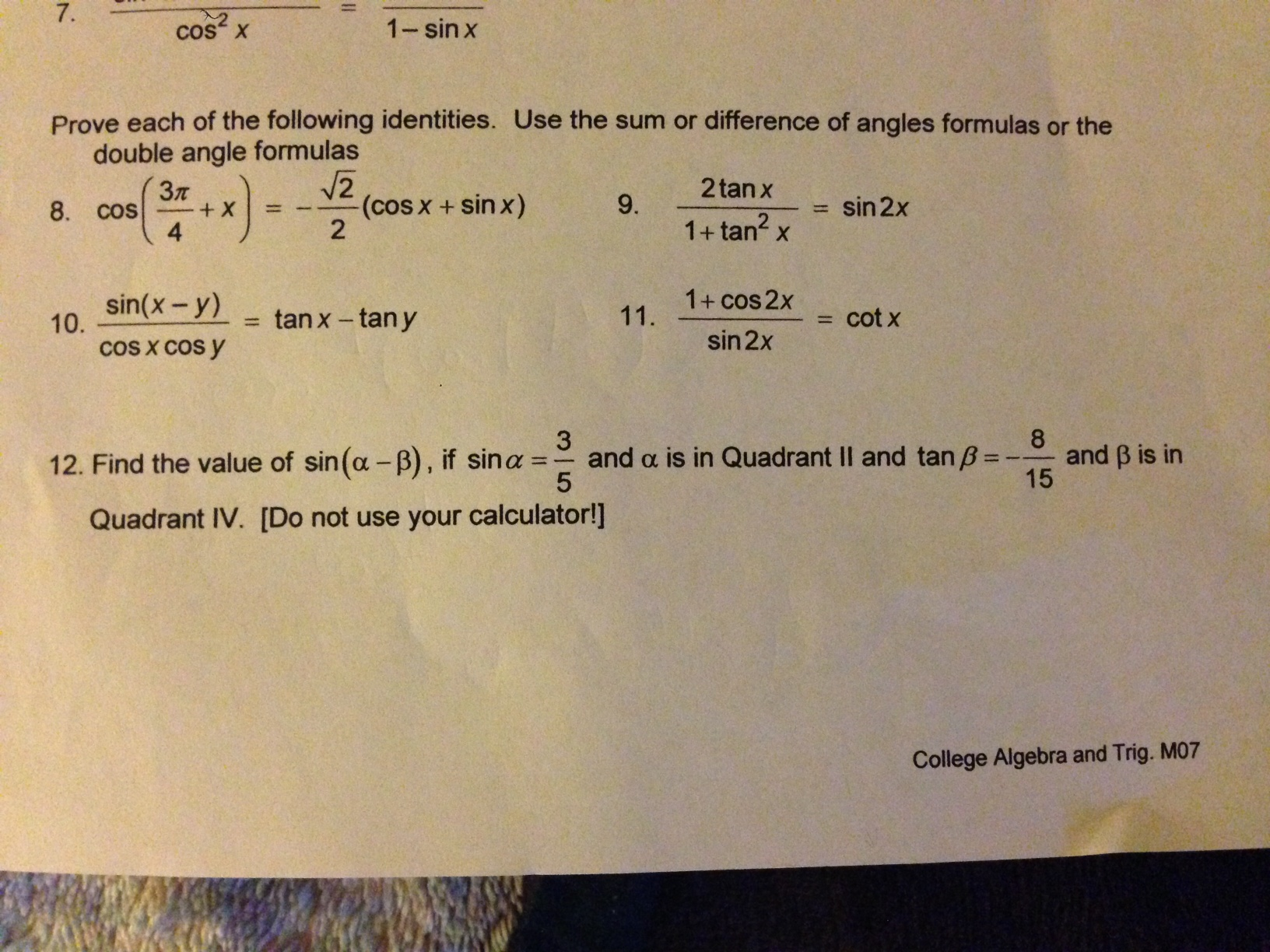
Prove Each Of The Following Identities Use The Sum Chegg Com

Leearlington Weebly Com Uploads 2 3 9 6 Precalculus Lesson 7 3c Pdf

Consider the expression sin3x We will use the addition formulae and double angle formulae to write this in a different form using only terms involving sinx and its powers We begin by thinking of 3x as 2xx and then using an addition formula wwwmathcentreacuk 3 c mathcentre 09Expand tan (4x) tan (4x) tan ( 4 x) Factor 2 2 out of 4x 4 x tan(2(2x)) tan ( 2 ( 2 x)) Simplify the numerator Tap for more steps Apply the tangent double angle identity 2 2 tan ( x) 1 − tan 2 ( x) 1 − tan 2 ( 2 x) 2 2 tan ( x) 1 tan 2 ( x) 1 tan 2 ( 2 x) Simplify the denominator2x 3x formula Proving Double angle formulas You are here Triple angle formulas Half angle formulas (Power reducing formulas) Ex 33, 24 Ex 33, 25 Ex 33, 23

Wl Apsva Us Wp Content Uploads Sites 38 15 05 Lesson 6 4 Notes 1 Pdf

How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube

The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are known as double angle formulae To understand this better, It is important to go through the practice examples provided Go through this article, and you will be able to derive the double angle formulae using the addition formulae The sine of 60 is (root 3) / 2 This is why your friend sine is so upset Let's test our double angle formula with the same angle So sin (2 x) is sin60 For our double angle formula = cos 2 x – 1 cos 2 x = 2cos 2 x – 1 For tan 2x Next Triple angle formulas→ Concept wise;

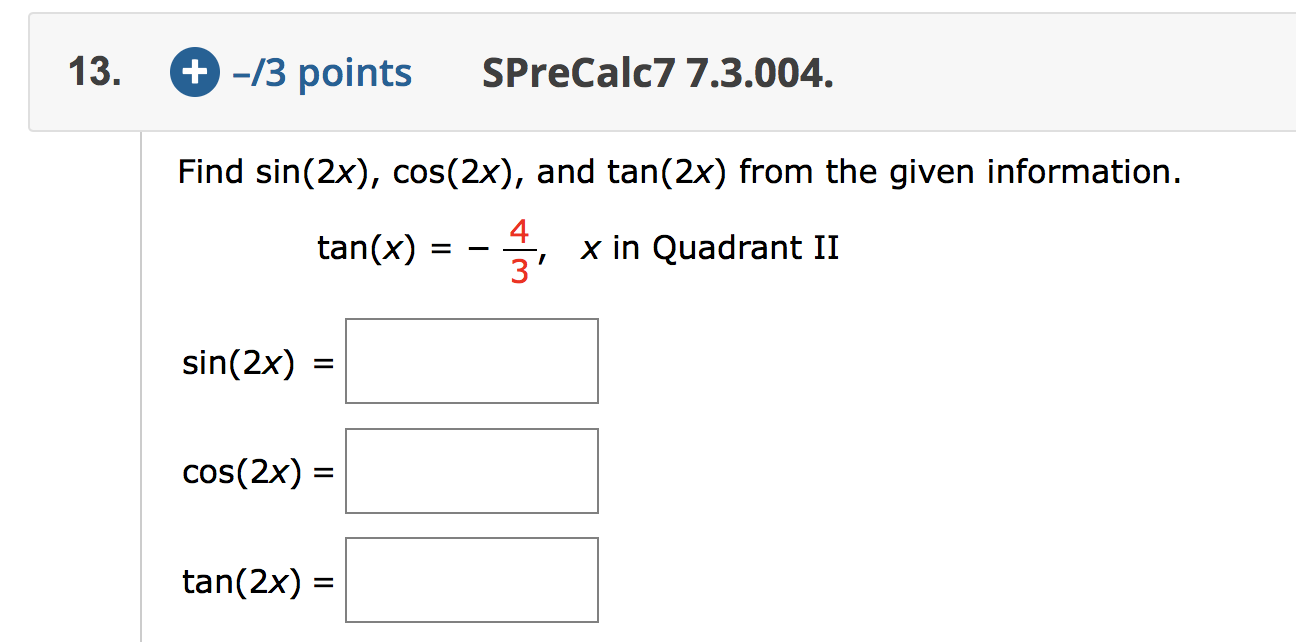
2 Points Sprecalc7 7 3 029 16 Simplify The Chegg Com

Double Angle Formulas Sin 2x Cos 2x Tan 2x Trigonometry Creata Classes Youtube

$\endgroup$ – Mike Pierce Dec '15 at 1712 $\begingroup$ @MikePierce It is not provided in my textbook, so it probably wants me to solve it without it $\endgroup$ –Problem Set 53 Double Angle, Half Angle, and Reduction Formulas 1 Explain how to determine the reduction identities from the doubleangle identity cos(2x) = cos2x−sin2x cos ⁡ ( 2 x) = cos 2 x − sin 2 x 2 Explain how to determine the doubleangle formula for tan(2x) tan ⁡ ( 2 x) using the doubleangle formulas for cos(2x) cosThe angle in the sin double angle formula can be denoted by any symbol Therefore, the following three are popular forms of sine of double angle identity in terms of tangent (1) sin 2 x = 2 tan

Ppt Double Angle And Half Angle Formulas Powerpoint Presentation Free Download Id

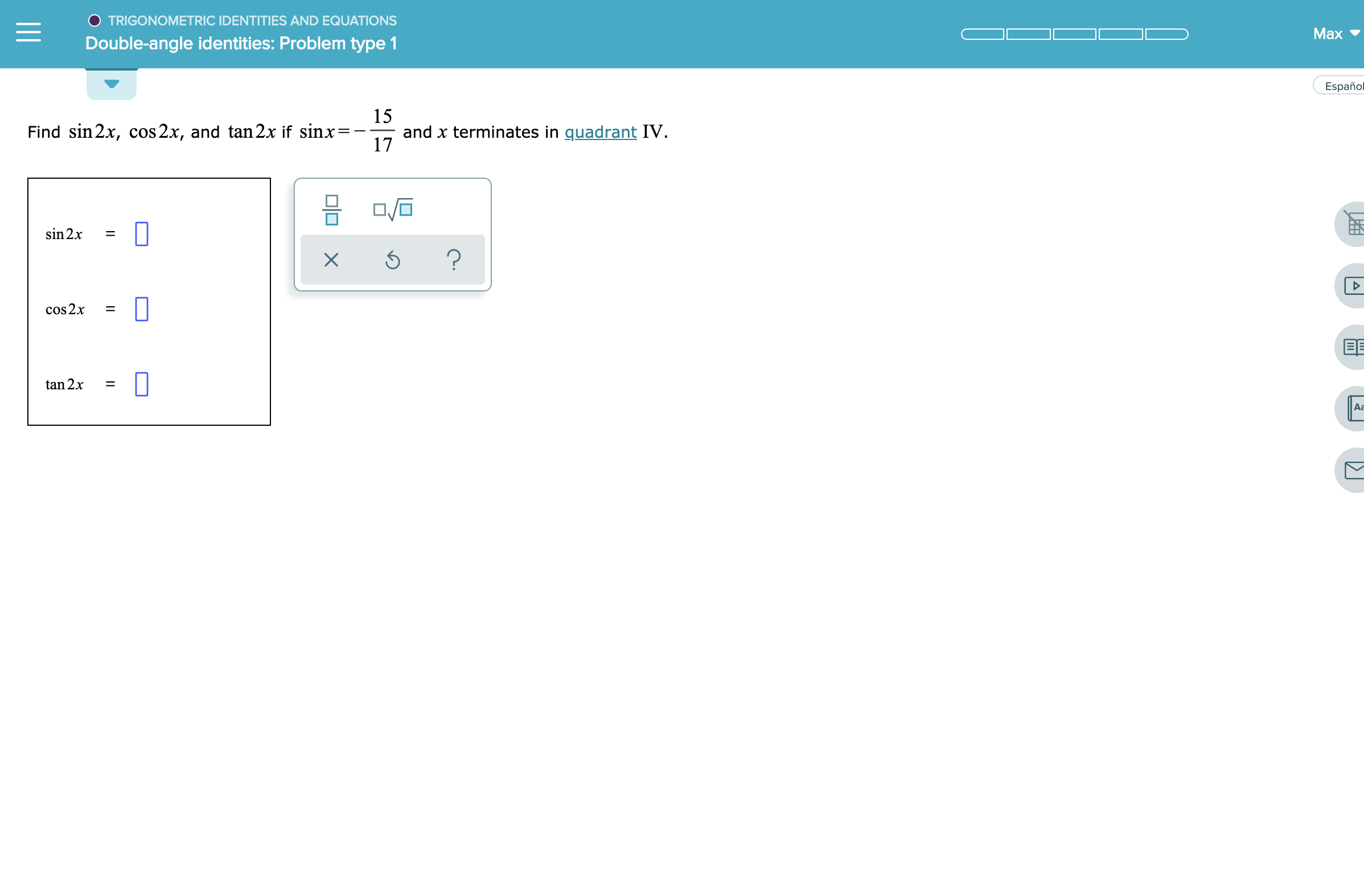
Answered O Trigonometric Identities And Bartleby

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Proof sin^2 (x)= (1cos2x)/2 Proof cos^2 (x)= (1cos2x)/2 Proof Half Angle Formula sin (x/2) higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50and put B = A to get tan(A A), or use

Double Angle Half Angle Formulas Ppt Download

Section 5 5 Multiple Angle And Half Angle Formulas

 This result is called the sine of a double angle It is useful for simplifying expressions later Cosine of a Double Angle Using a similar process, we obtain the cosine of a double angle formula cos 2α = cos 2 α − sin 2 α Proof This time we start with the cosine of the sum of two angles cos(α β) = cos α cos β − sin α sin β,For example, using these formulas we can transform an expression with exponents to one without exponents, but whose angles are multiples of the original angle We obtain halfangle formulas from double angle formulas Both sin (2A) and cos (2A) are derived from the double angle formula for the cosine cos (2A) = cos 2 (A) − sin 2 (A) = cos 2The figure at the right shows a sector of a circle with radius 1 The sector is θ/(2 π) of the whole circle, so its area is θ/2We assume here that θ < π /2 = = = ⁡ = ⁡ The area of triangle OAD is AB/2, or sin(θ)/2The area of triangle OCD is CD/2, or tan(θ)/2 Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we have

5 Tan 2x Cos 2x 2cos2x 9 Find Cos4x Iit Jee Trigonometry Double Angle Youtube

Double Angle Formula Tan Youtube

Double angle formula for tangent tan2x = 2tanx/1tan^2x Formula for arc length To find the value of sin2x × Cos 2x, the trigonometric double angle formulas are used For the derivation, the values of sin 2x and cos 2x are used So, Sin 2x Cos 2x = 2 Cos x (2 Sin x Cos2 x − Sin x) Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin ⁡ \sin sin and

Section 6 3 Double Angle And Half

Www Rusdlearns Net C File Show

 Use tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x, for the right hand side expression 2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x) =2 sin x cos x/(cos^2xsin^2x) =(sin 2x)/(cos 2x)=tan 2x Proofs for sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x Use Area of a triangleABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the triangle ABC of a unitTan 2x ≠ 2 tan x by Shavana GonzalezTrigonometric Simplification Calculator \square!

Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com

Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

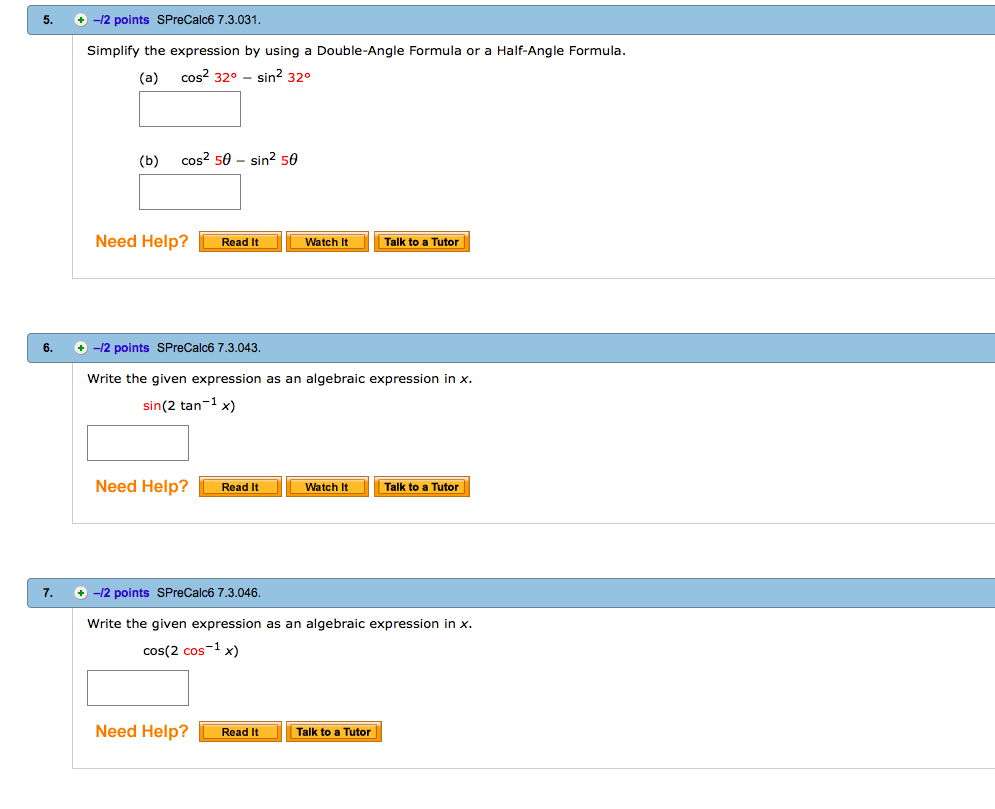
Now, sin(2x) is 2sin(x)×cos(x), that's the double angle formula for sine00 Of course, you find that out from the addition formula09 Cos(2x) is cos 2 (x)sin 2 (x), that was the first double angle formula for cosine02 Now, it's not totally obvious how to proceed next, but I know that I'm trying to get everything in terms of tan(x)0844Answer to Double Angle Formulas Find sin 2x, cos 2x, and tan 2x from the given information, x in Quadrant II2 Find the value of the unknown angle 3 Once you find the value of your angle, subtract it from 180° to find the possible second angle 4 Add the new angle to the original angle If their sum is less than 180°, you have two valid answers If the sum is over 180°, then the second angle

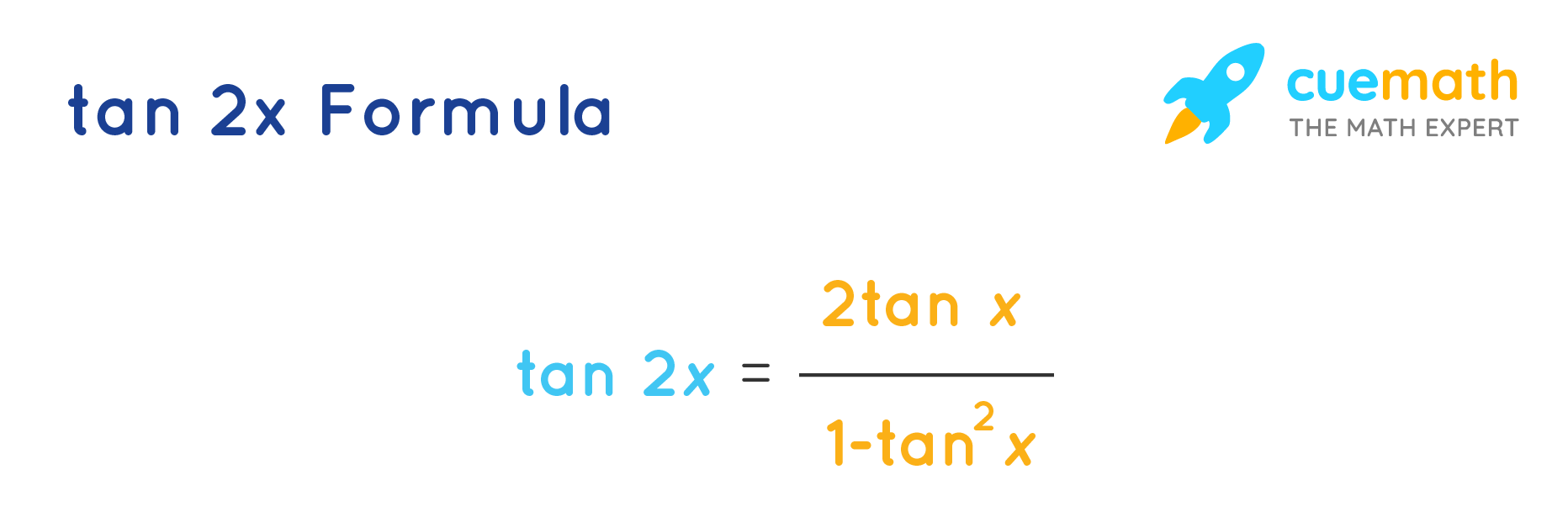
Tan 2x Formula What Is Tan 2x Formula Examples

Http Www Cbsd Org Cms Lib010 Pa Centricity Domain 40 5 5 double angle formulas Pdf

Ppt Double Angle And Half Angle Identities Powerpoint Presentation Free Download Id

Double Angle And Half Angle Identities Lecture Notes Math 1b Docsity

Derivative Rules For Trigonometric Functions

Double Angle Formula Sine Cosine And Tangent Owlcation

Ppt Find Sin 2x Cos 2x And Tan 2x From The Given Information Image Select The Correct Answer Powerpoint Presentation Id

Www Jensenmath Ca Unit 5 pretest review solutions Pdf

Quiz Worksheet Double Angle Formula Study Com

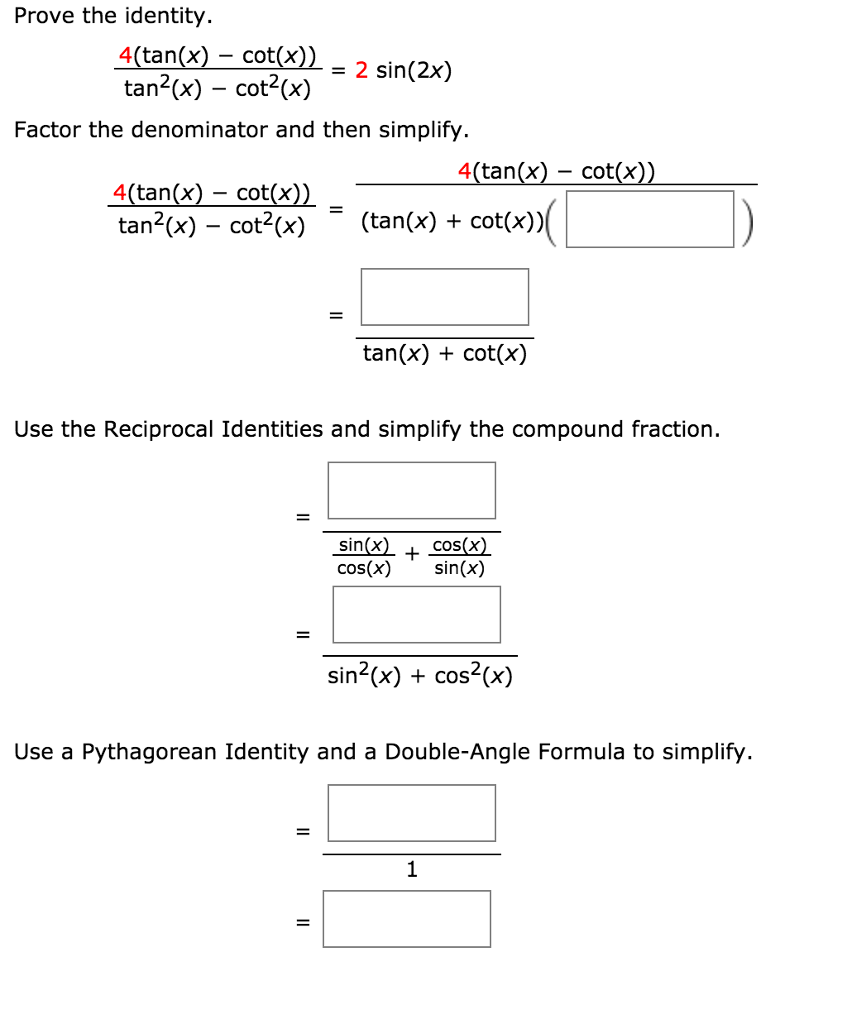
Prove The Identity 4 Tan X Cot X Tan 2 X Chegg Com

1

Prove Trigonometric Identity Using Double Angle Formula Youtube

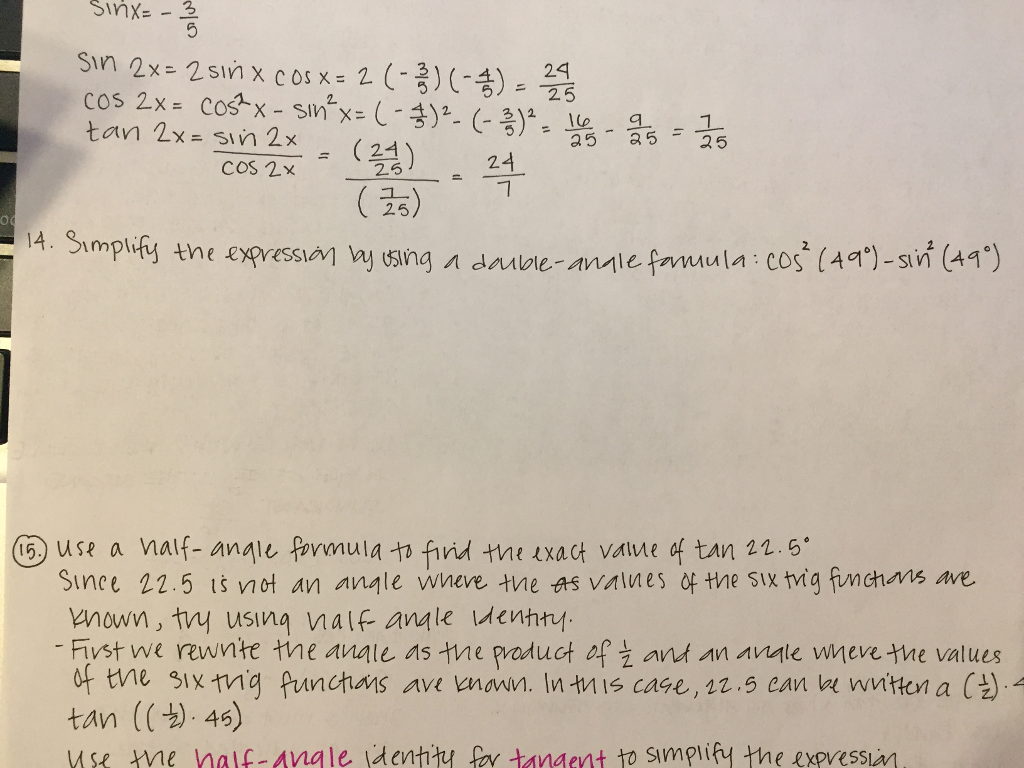
Solved Simplify The Expression Using The Double Angle For Chegg Com

Answered 4 Find The Exact Value Do Not Use A Bartleby

Double Angle And Half Angle Formulas Ppt Download

1

7 3 Da Ha Red Sine Trigonometric Functions

Trigonometric Identities Trigonometric Functions Trigonometry

Lesson 4 5 Double Angle Formulas

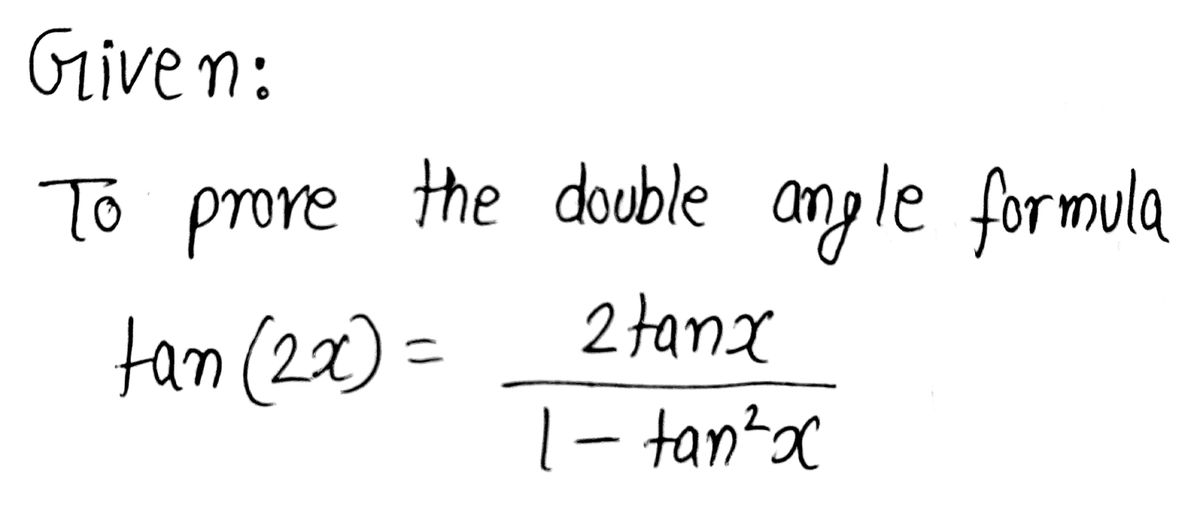
Answered Can You Guide Me Though The Proof Of Bartleby

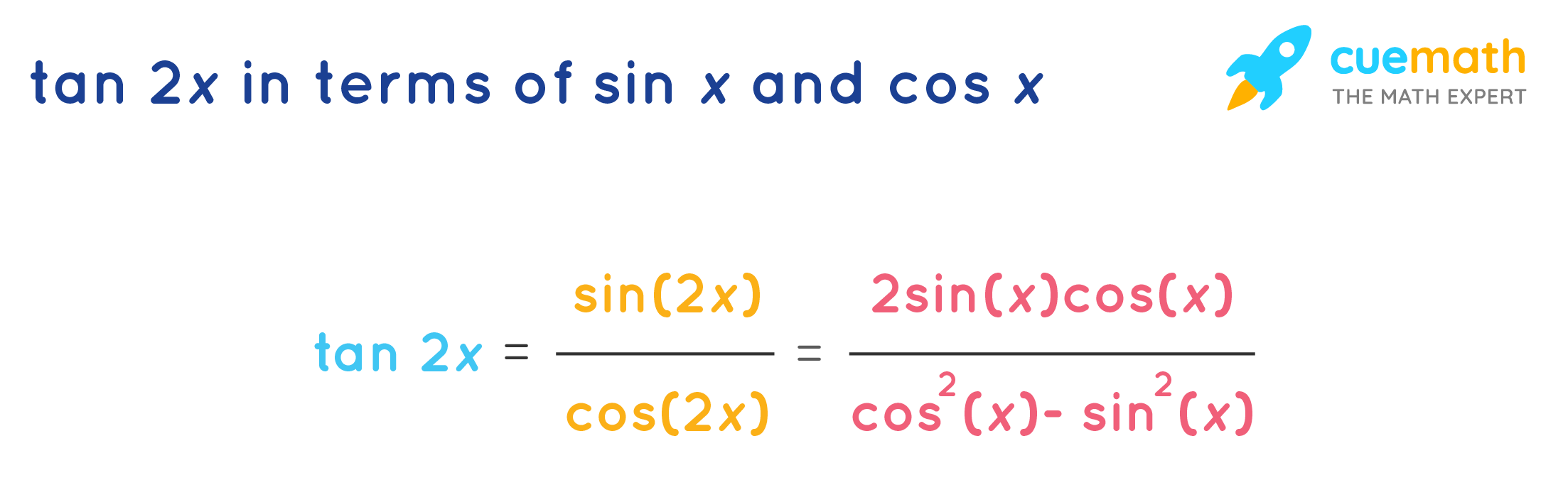
Tan 2x Formula What Is Tan 2x Formula Examples

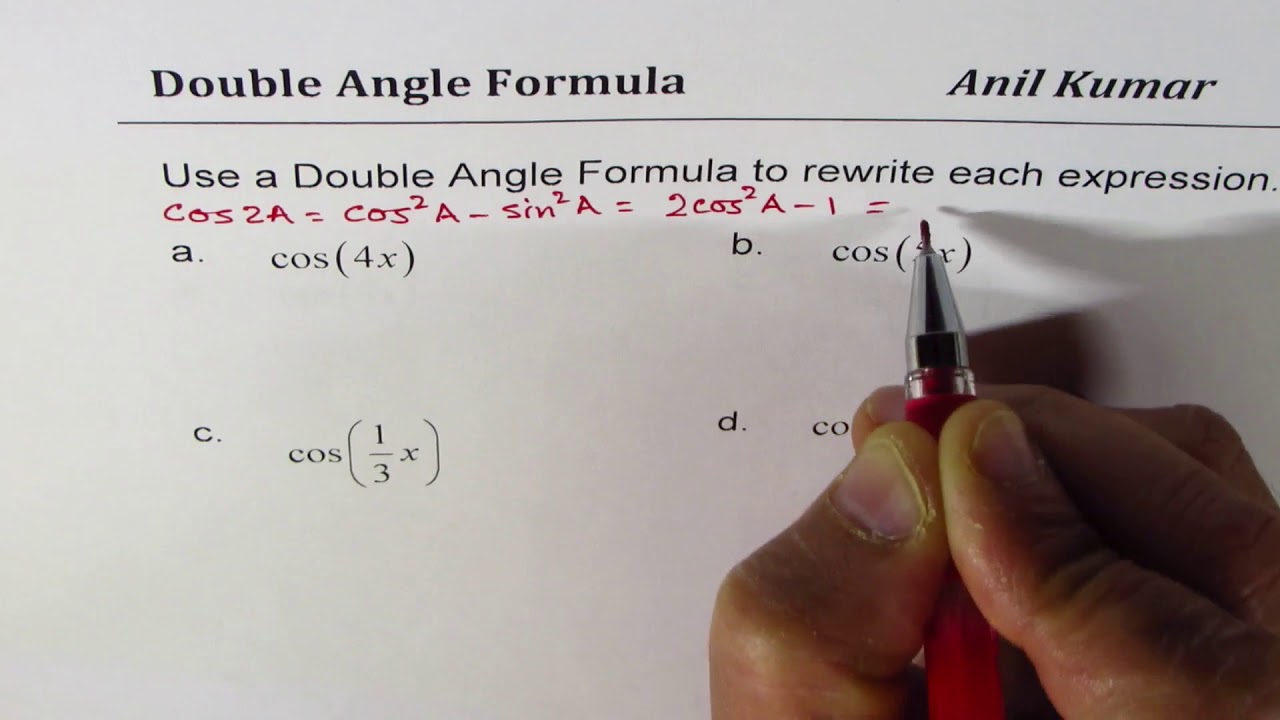
Cos 4x Sin 3x Tan X 2 Use Double Angle To Rewrite Trigonometric Expressions Youtube

Ppt Double Angle And Half Angle Formulas Powerpoint Presentation Free Download Id

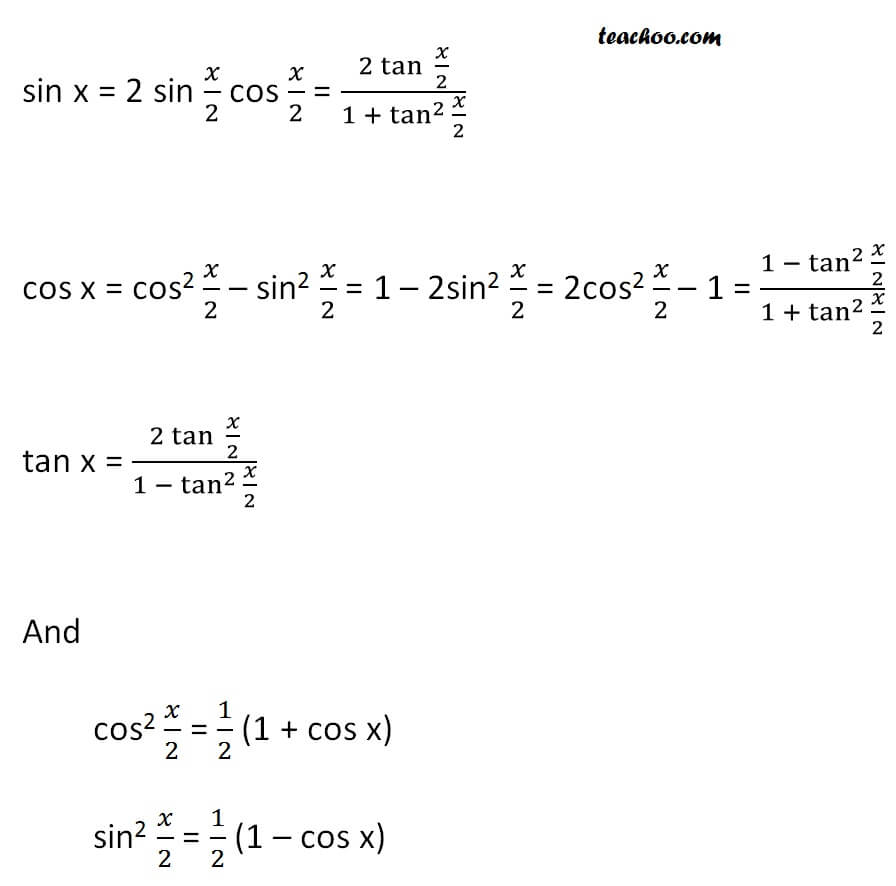
Half Angle Formulas Power Reducing Formulas 2x 3x Formula Provin

1 Sin 2 X Formula Sepertikisahku

Lecture 129 Proof Half Angle Formula Tan X 2 Cosmolearning Mathematics

Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube

Section 7 3 Double Angle Half Angle And Chegg Com

2

2

Ppt Analytic Trig Powerpoint Presentation Free Download Id

Tan 2x Tan 2x

Http Www Cbsd Org Cms Lib Pa Centricity Domain 40 5 5 double and half angle formulas notes Pdf

Math2412 Double Angle Power Reducing Half Angle Identities Pdf Trigonometric Functions Sine

Trigonometric Identities And Formulas V2 0 Trigonometric Functions Sine

Http Theprofessorshut Weebly Com Uploads 2 3 2 7 Pc Chap 6 Sect 3 Double And Half Angle Identities Pdf

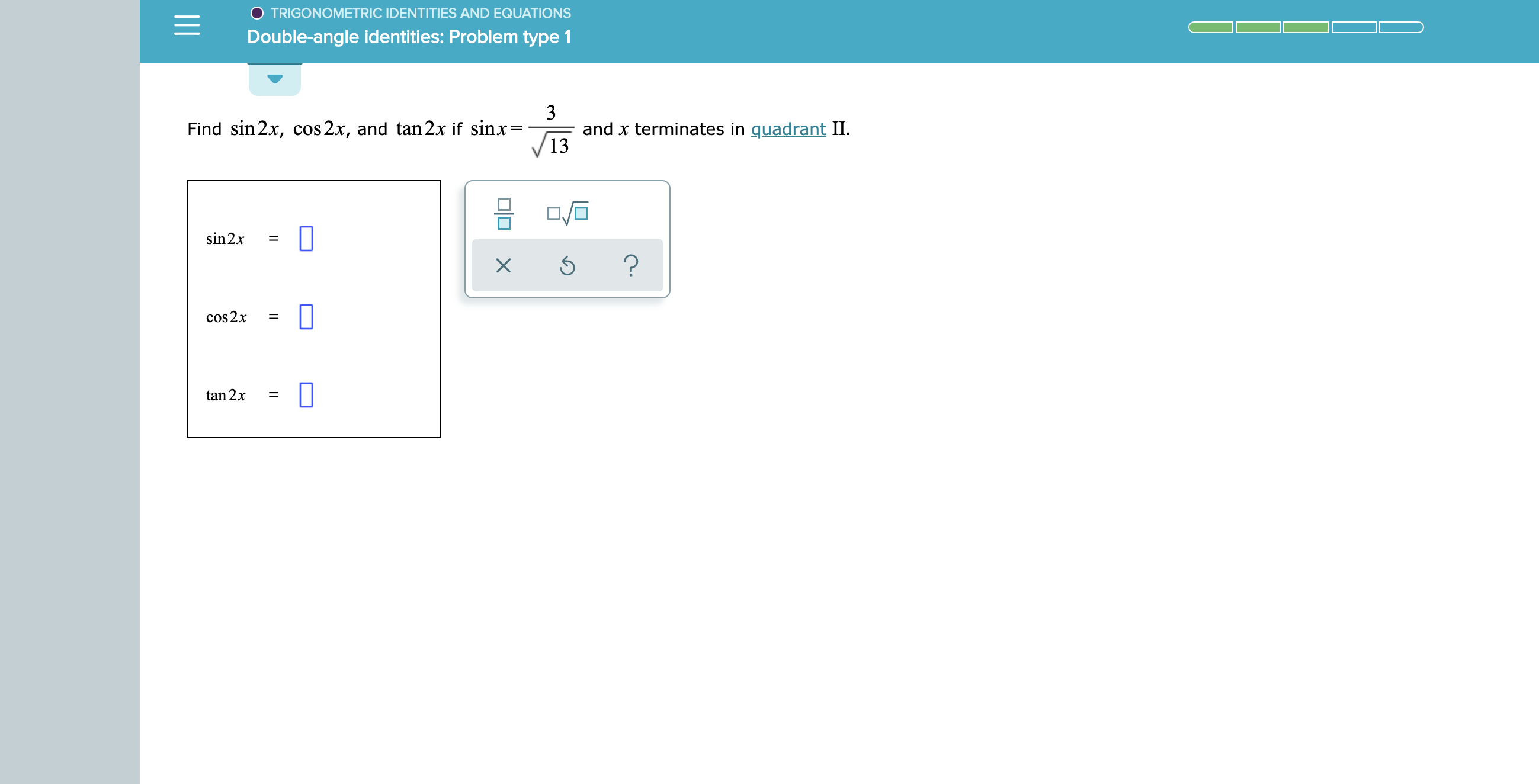
Answered Trigonometric Identities And Equations Bartleby

Lesson 52 Double Angle Half Angle Identities Ppt Download

2

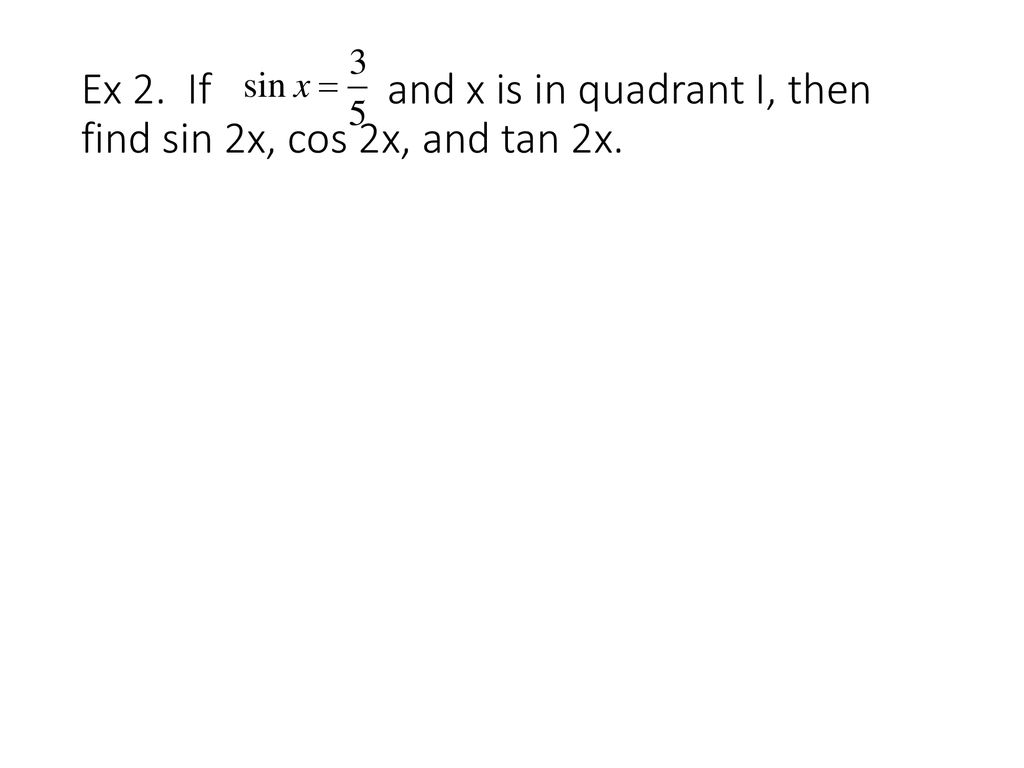
Double Angle Half Angle Formulas Ppt Download

Solving Trigonometric Equations Ppt Download

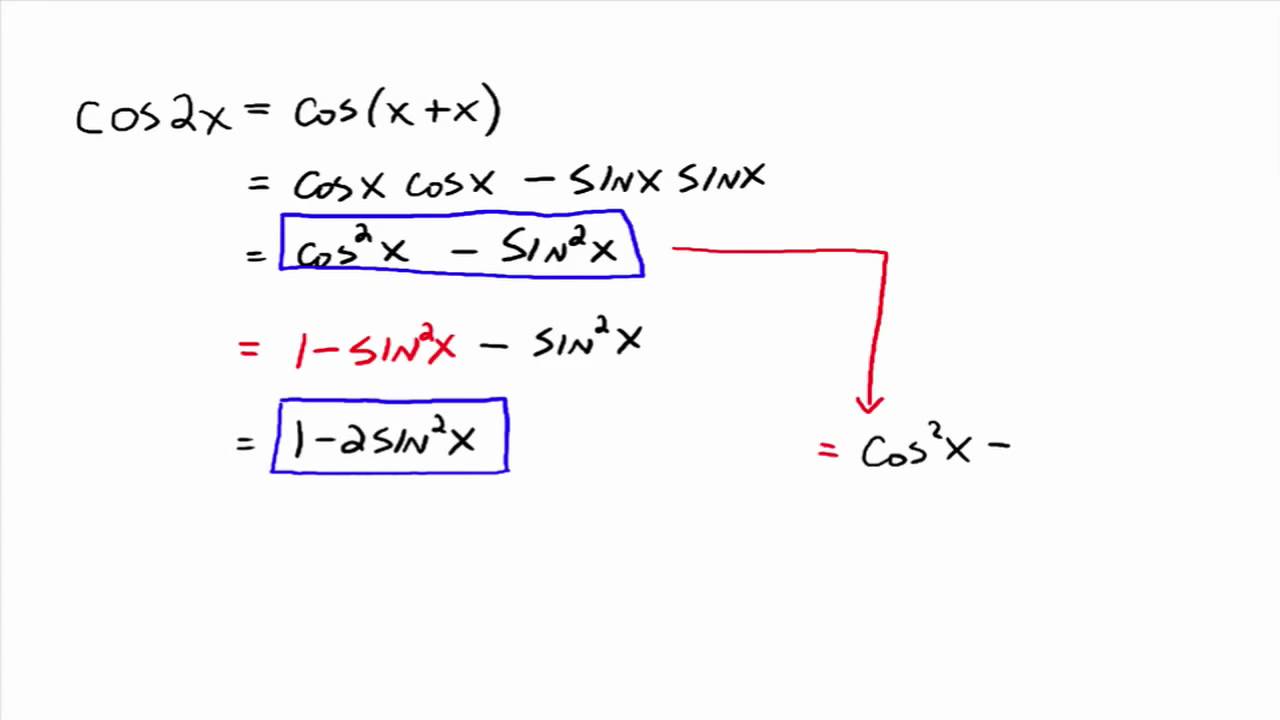
Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

3 4 2 Double Angle Identities K12 Libretexts

3 4 2 Double Angle Identities K12 Libretexts

Http Www Pstcc Edu Facstaff Jwlamb 1730 7 3 Pdf

Http People Clas Ufl Edu Chui Files F13l3 Trig Integrals Part I Pdf

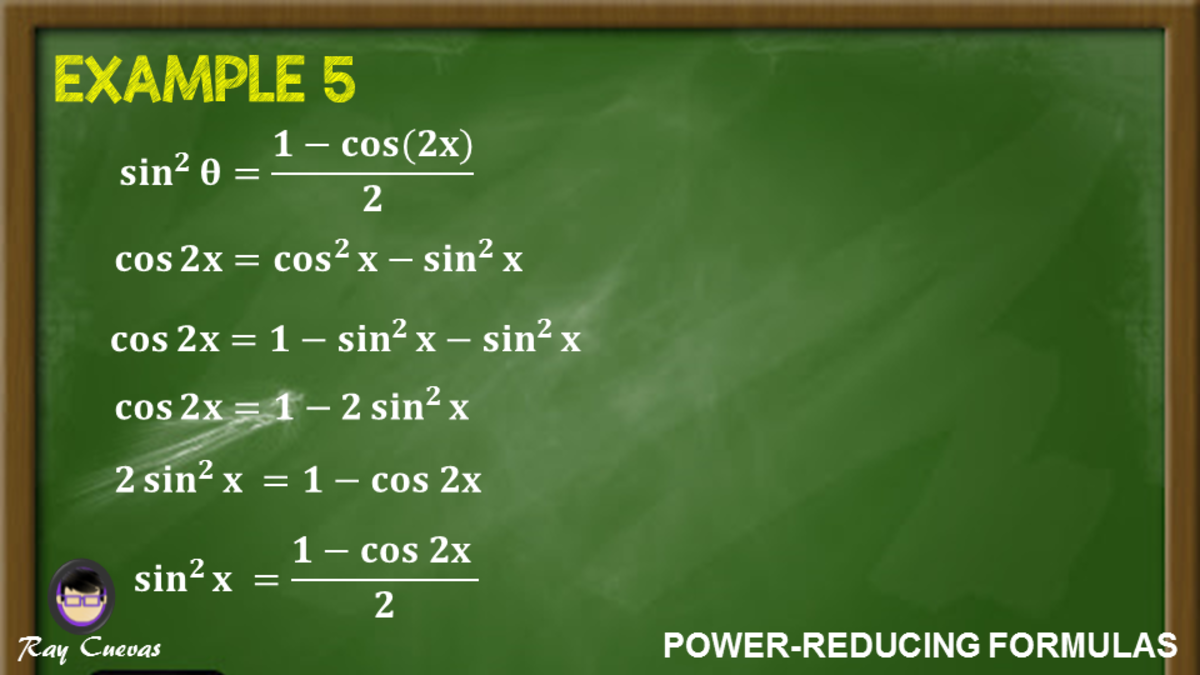
Power Reducing Formulas And How To Use Them With Examples Owlcation

1 14 Points Sprecalc6 7 3 004 Find Sin 2x Cos 2x Chegg Com

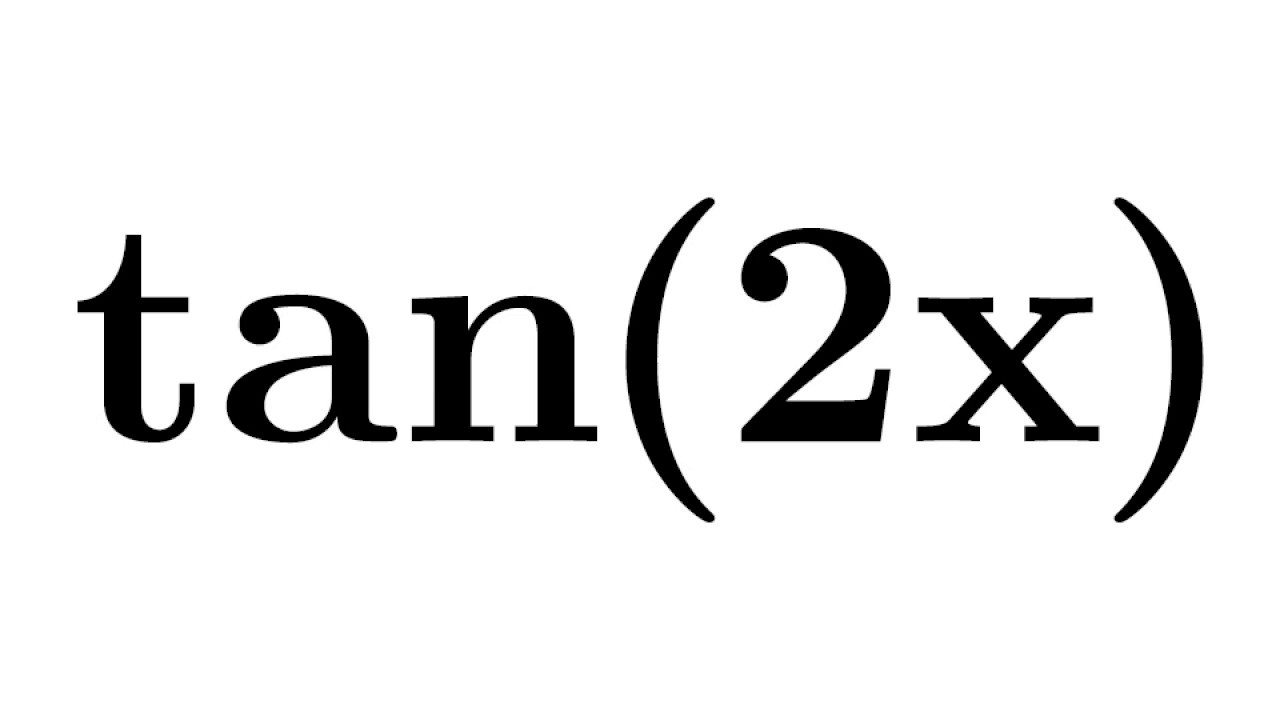
Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube

Pre Calculus Using The Double Angle Of Tangent To Solve An Equation Youtube

2

Chapter8 Circles 2 Pages 251 300 Flip Pdf Download Fliphtml5

1 Sin 2 0 Cos 2x 1 Tan 3 To Prove That 1 Tan 2 Chegg Com

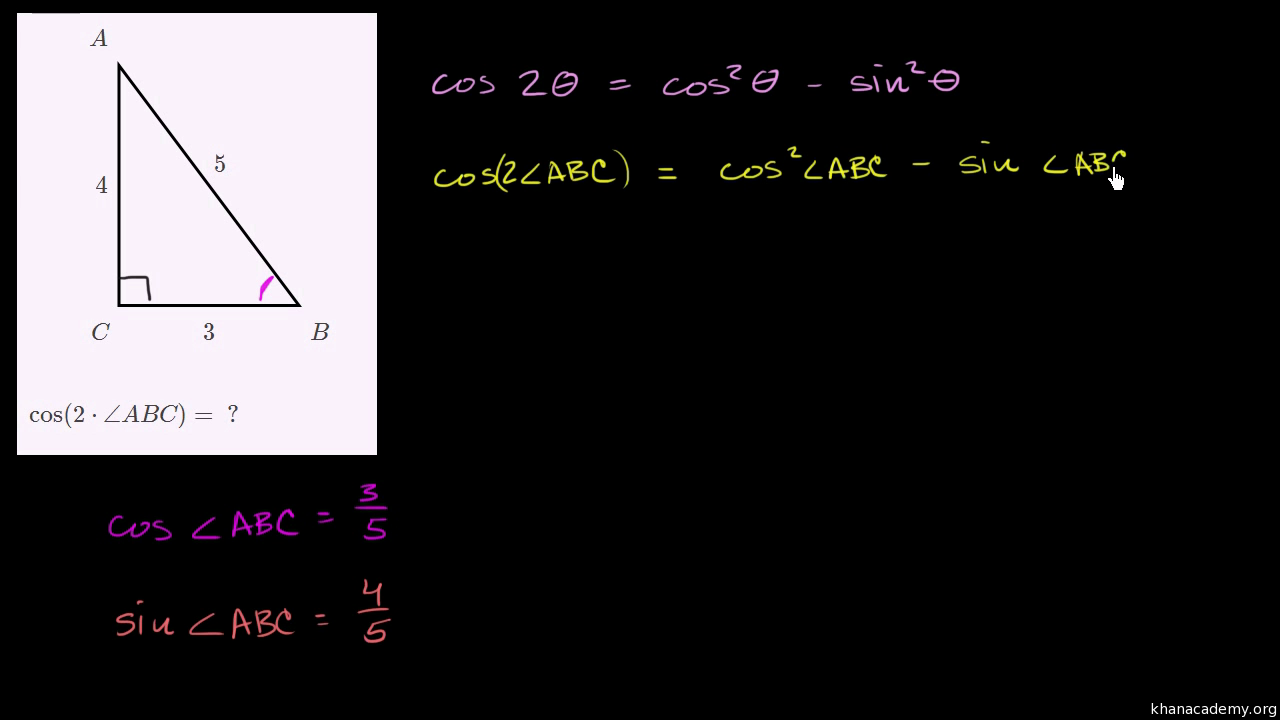
Double Angle Formulas Using Cosine Double Angle Identity Video Khan Academy

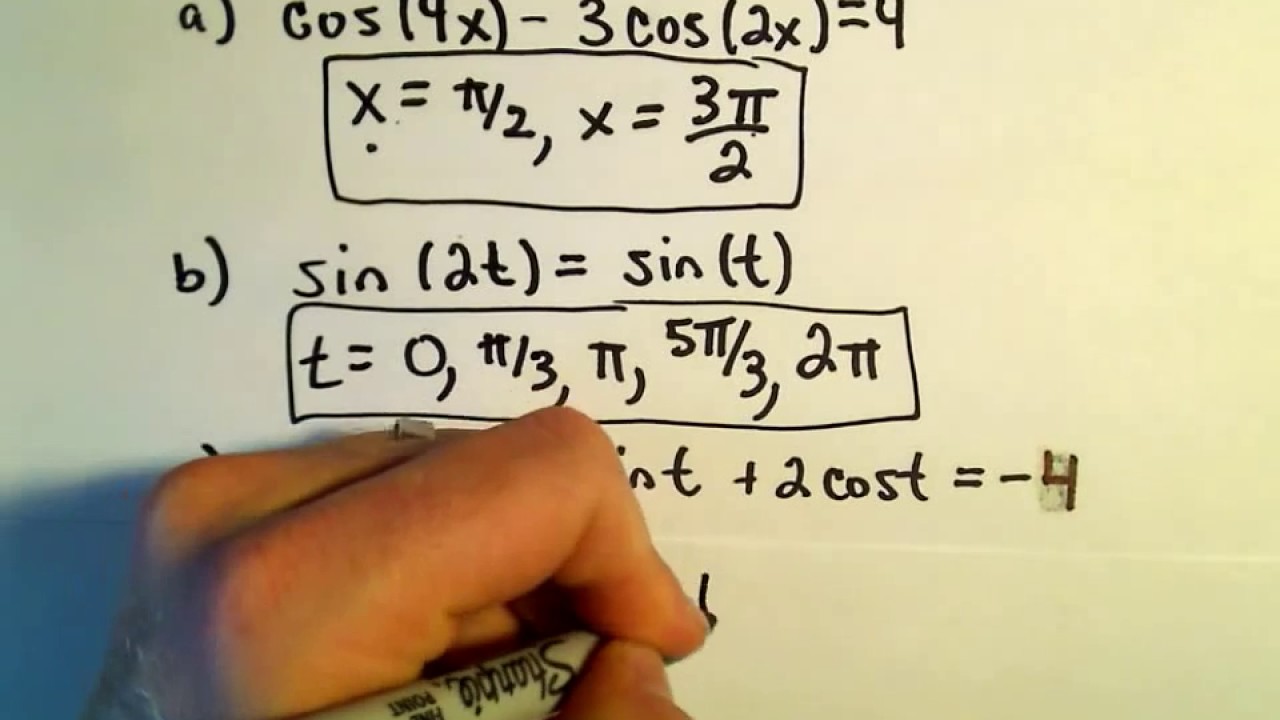
Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

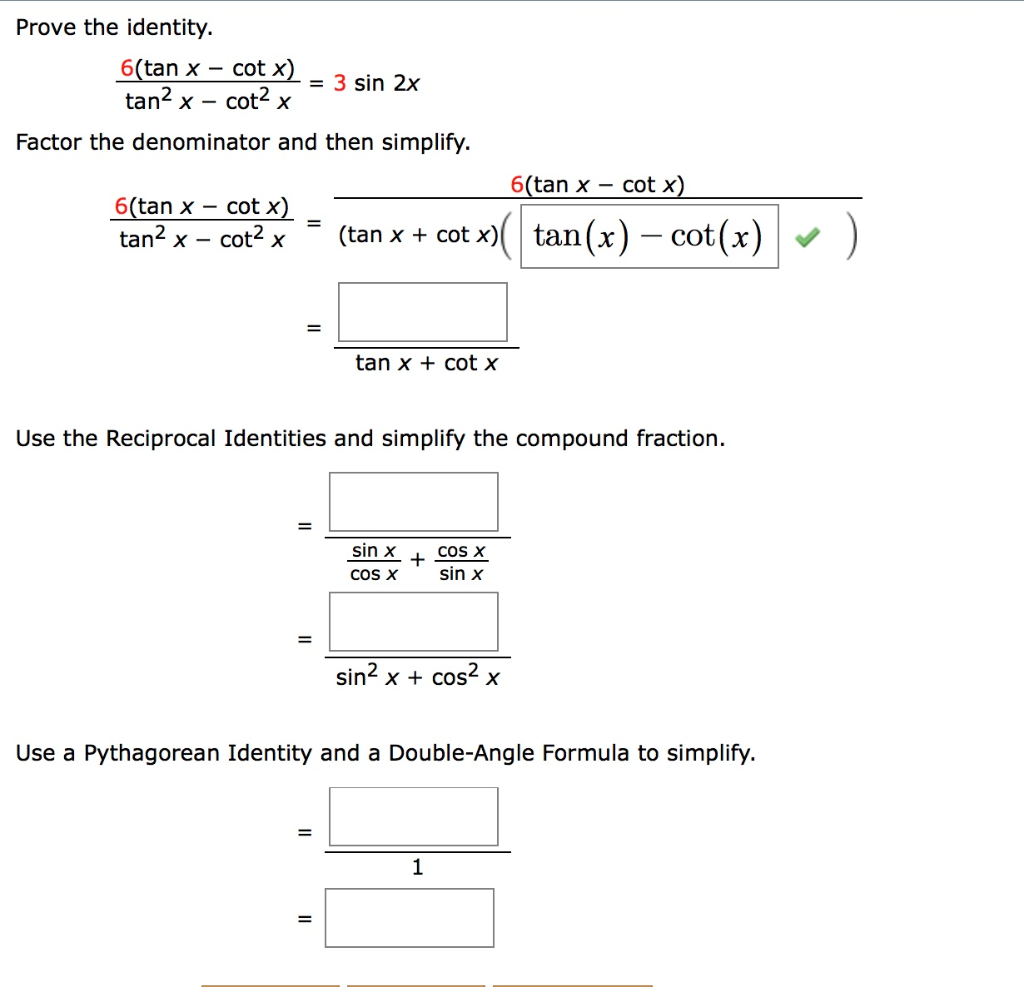
Prove The Identity 6 Tan X Cot X Tan2 X Cot2 X Chegg Com

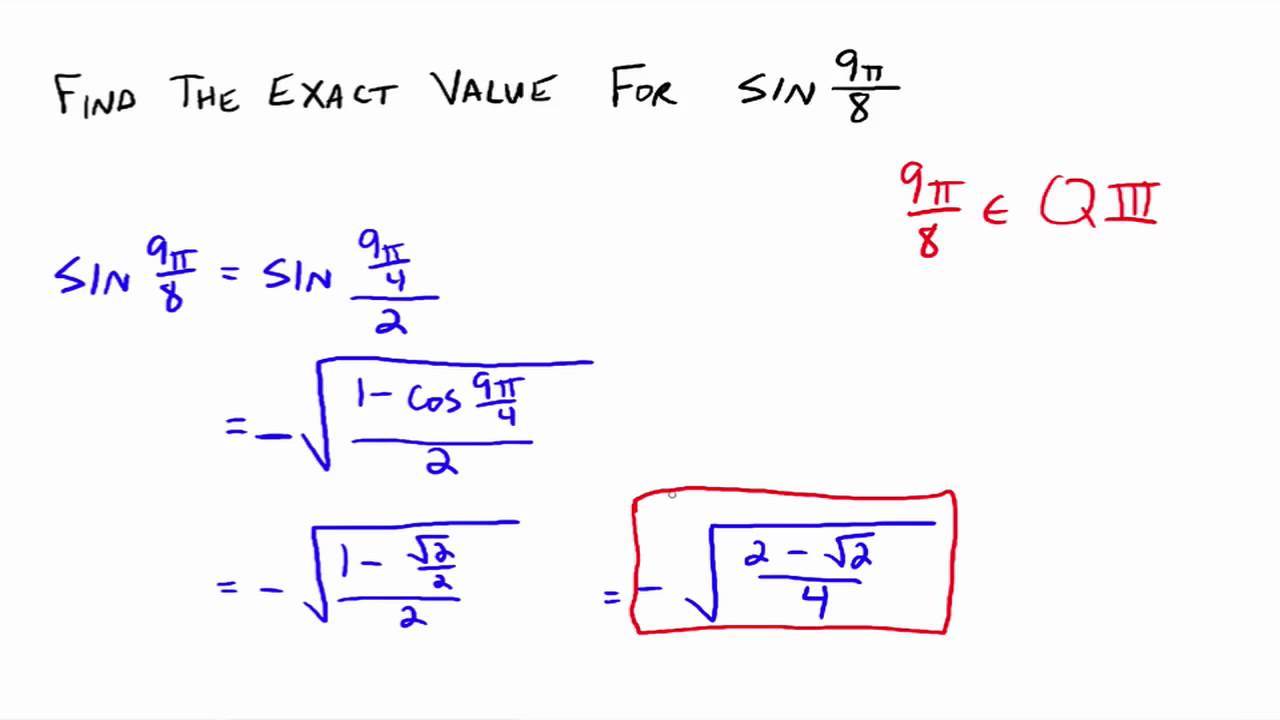
Double Angle And Half Angle Formulas With Worked Solutions Videos

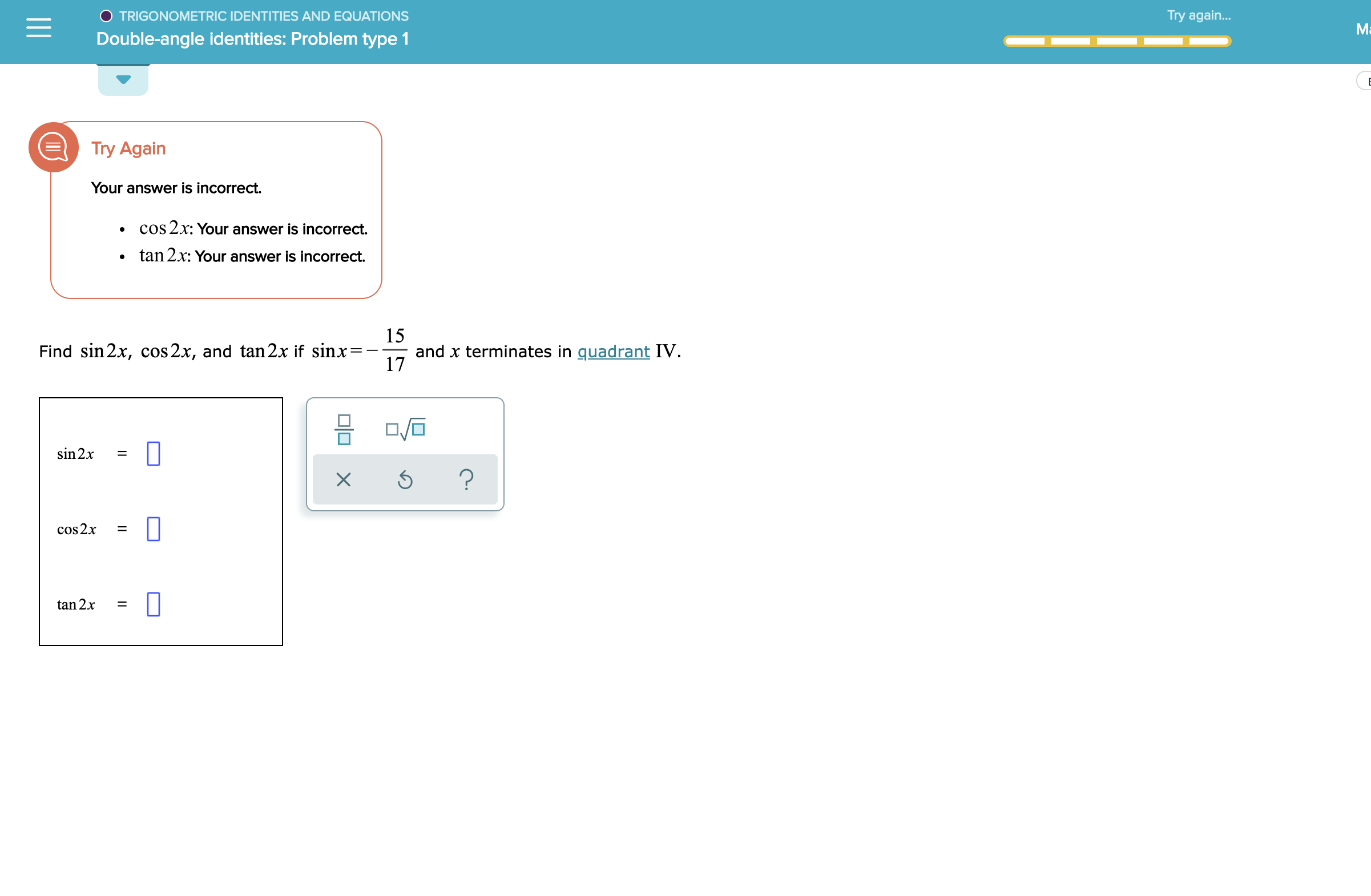
Answered O Trigonometric Identities And Bartleby

Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf

56 Questions On Double Angle And Half Angle Formula Precalculus Math 1330 Docsity

Double Angle Formula Sine Cosine And Tangent Owlcation

2

Http Www Fortbendisd Com Cms Lib09 Tx Centricity Domain 7344 Double angle identities answer key Pdf

1

Examples Double Angle Formulas Ppt Download

2

Cosx 3 5 Find Tanx 2 Half Angle Tangent Formula Derivation With Important Example Youtube

Http Www Mayfieldschools Org Downloads 4 8 double angle formulas key Pdf

Http Www Anderson1 K12 Sc Us Cms Lib04 Sc Centricity Domain 1150 S15 hpc trig review keys Pdf

Double Angle Identities Formula In Trigonometry In Hindi Urdu Full Hd Youtube

Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath

Double Angle Formulas What Are Double Angle Formulas Examples

3 Use Double Angle Formulas To Find The Exact Value Chegg Com

7 4 Double Angle And Half Angle Identities Flip Ebook Pages 1 2 Anyflip Anyflip

Wl Apsva Us Wp Content Uploads Sites 38 15 05 Lesson 6 4 Notes 1 Pdf

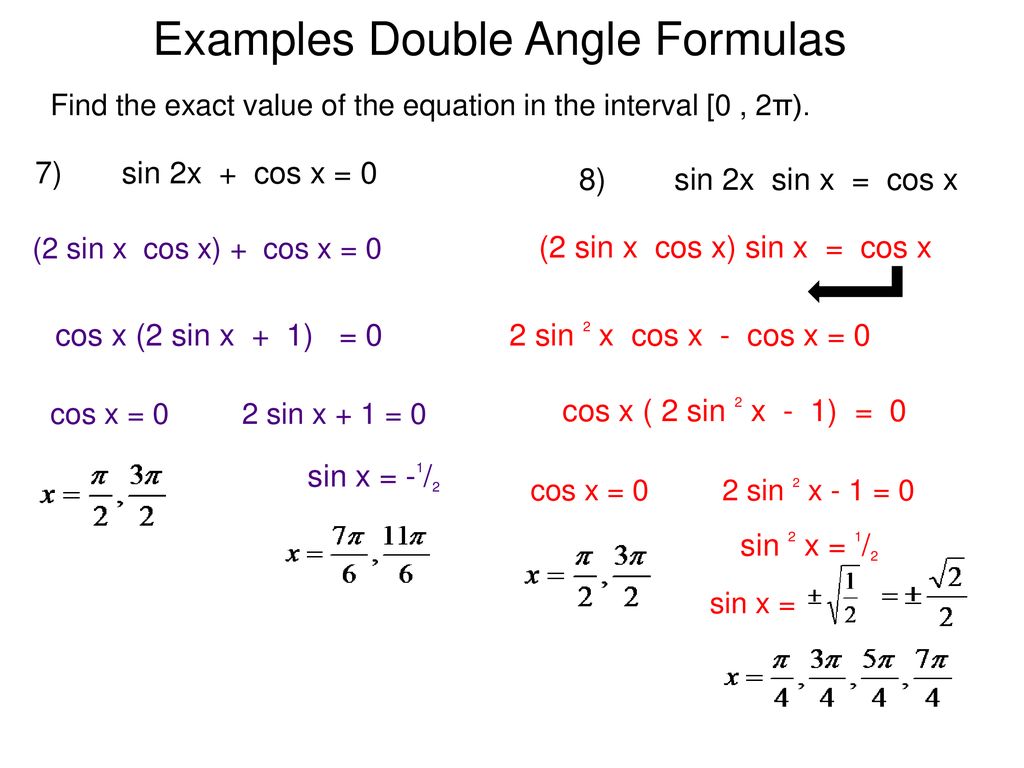
Examples Double Angle Formulas Ppt Download

Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau

Trig Find Tan X Given Tan 2x 2 Pi X 3pi 2 Cheatatmathhomework

2

9 3 Other Identities Ppt Download

Incoming Term: tan 2x double angle formula,